В основу классической дарвинской теории биологической эволюции положено представление о том, что изменение форм происходит за счет мелких случайных уклонений под непрерывным контролем естественного отбора. Такое объяснение подразумевает, что эволюционный процесс есть медленное, непрерывное развитие, настолько медленное, что практически незаметно на том сравнительно небольшом отрезке времени, на котором его можно непосредственно изучать. Эта теория, получившая в своем дальнейшем развитии наименование синтетической эволюционной теории, способна так или иначе объяснить большинство фактов и явлений, определяющих эволюционный процесс.
Однако объяснение, в отличие от доказательства, не закрывает путей к дискуссии, поэтому неудивительно возникновение различного рода гипотез, трактующих с других позиций те или иные моменты биологической эволюции. Тем более, что имеется ряд положений, которые в рамках самой синтетической теории либо, по разному объясняются различными исследователями, либо признается, что объяснение данного факта является предположительным.
Прежде всего это относится к проблеме видообразования, которую Дарвин считал основной в теории эволюции [1]. Эта проблема до сих пор служит примером кардинальных расхождений ведущих эволюционистов – от полного отрицания симпатрического видообразования и постулирования ведущей роли периферических изолят [2], до утверждения ее эволюционной бесперспективности [3]. Неоднозначно и отношение специалистов к роли межвидовой конкуренции в процессе видообразования. Так Майр игнорирует это явление, в то время как Гаузе считает его одним из основных факторов эволюции [4].
Серьезные сомнения вызывает описание, в рамках классической теории биологической эволюции, процесс образования новых признаков. Хотя Северцев и Майр дали этому явлению два различных объяснения в рамках классической теории [2], с выходом биологии на молекулярный уровень и открытия генетического мономорфизма, подобные сомнения вновь возродились, получив экспериментальную поддержку [5,6].
Парадокс скорости эволюции. Практически во всех работах, затрагивающих эту проблему, при переходе от общих рассуждений к количественным оценкам, скорость эволюции определяется как величина пропорциональная трем основным параметрам: коэффициенту отбора, величине популяции и частоте смены поколений [1, 7]. В этом случае логично ожидать, что скорость эволюции, должна быть выше у организмов с большей частотой смены поколений, а так же у более многочисленных организмов, тем более, что в классической теории постулируются именно малые значения коэффициента отбора.
В природе же наблюдается скорее обратная закономерность. Такие высшие организмы как гоминиды, хоботные, китообразные, прошедшие несомненно большой эволюционный путь, имеют сравнительно низкую численность и длинный репродукционный цикл.
Другим трудно объяснимым, в рамках классической теории, свойством эволюционного процесса, является крайняя неравномерность ее течения в пределах каждой отдельной филетической линии, а так же большие различия в скорости эволюции в различных группах. Крайнее выражение этого свойства состоит в наличии консервативных групп, так назывемых «живых ископаемых». Хотя в ряде работ этому явлению дается объяснение в рамках классической теории, тем не менее, по словам Майра [2], «явления эволюционного застоя всегда были загадкой».
Таким образом, уже эти примеры свидетельствуют об определенных затруднениях в концепции о постепенном восхождении организмов по эволюционной лестнице. При этом, основная трудность заключается в постулируемом непрерывном давлении естественного отбора, не позволяющего закрепиться переходным вариантам, не обладающим адаптивным преимуществом.
Хотя, как говорилось выше, в рамках классической теории существует объяснение практически всех явлений эволюции, однако это часто достигается за счет довольно сложных и не всегда убедительных, а иногда и противоречащих друг другу конструкций (географическая и другие изоляции, дизруптивный отбор, половой отбор и пр.).
Более того, практически все исследователи классического направления вводят механизмы, позволяющие случайным образом сдвинуть генетические частоты и тем самым избежать непрерывного давления естественного отбора. Использование в качестве эволюционных факторов дрейфа генов, волн жизни, принципа основателя и квантовой эволюции – все это попытки «обмануть» отбор, хотя бы на время уменьшить его консервативное влияние.
Поэтому, в эволюционном смысле, был бы полезен механизм, позволяющий выводить из под контроля естественного отбора тот или иной признак или совокупность признаков, с тем чтобы эти признаки могли пройти определенную стадию развития, включающую в себя состояния менее адаптивные и даже летальные. Здесь понятие «выведение из под контроля естественного отбора» эквивалентно понятию «выведение из под жизнобеспечения». Такое положение должно сохраняться до тех пор пока эти признаки не приобретут значения повышающие адаптивность организма. Тогда, после включения их в жизнеобеспечение, естественный отбор определит выбор между старой и новой формами.
В этом направлении существует ряд гипотез, например гипотеза об эволюционном значении генных дупликаций. Эта гипотеза основана на наличии в геноме высших организмов большого количества избыточного материала, состоящего частично из дупликаций известных локусов, частично из участков, имеющих «бессмысленный» код.
Важность дупликаций генов для биологической эволюции отмечалась еще исследователями школы Моргана. Мёллер и Бриджес важность того, что «дупликации позволяют ставить ранее запрещенные эксперименты, освобождая их от давления естественного отбора» [7]. В 1930 г. Н.П. Дубинин развивает представление о большой роли дуплицированных генов, предложив называть их «генами свободными в своей эволюции». Дальнейшее развитие в поддержку этих идей находим у ряда исследователей [3, 6-8]. Более того, известный генетик С. Оно считает генетические дупликации основной движущей силой эволюции.
Первоначально дупликации могут использоваться для увеличения производства соответствующего белкового материала или в качестве дублирующих элементов для повышения надежности [5]. Однако, если жизнеспособность организма существенным образом не снижается при отсутствии или уменьшении количества дублей, то мутации могут постепенно изменять их информационное содержание. По мере накопления изменений эти дубли становятся неспособными выполнять свою первоначальную роль, превращаясь в бессмысленный код. С этих пор, их единственная роль в организме – эволюционная.
Остается вопрос о распространении в популяции особей, получивших таким новое эволюционное качество.
Рассмотрим статистический механизм изменения некоторого признака на шкале его логических возможностей. Будем считать этот признак нейтральным. Переход из одного значения в другое производится в результате серии последовательных мутаций и дрейфа. Для простоты будем считать, что эта шкала не имеет ветвлений.
Пусть, в какой-то момент, все особи некоторой популяции имеют единое значение некоторой дупликации локуса. Ввиду того, что эта дупликация выведена из-под контроля естественного отбора, это значение будет «размываться» мутациями. Однако это «размывание» будет неполным, как в случае обычной диффузии. Статистический процесс рождения и гибели приводит к тому, что реальные значения признака будут блуждать по шкале его значений, в виде непрерывной группы, включающей в себя ограниченный диапазон значений (распределение значений).
Значения этой же дупликации в другой популяции будут блуждать в виде своей независимой группы.
Математическое описание этого эффекта дано в работах Морана, Ота и Кимуры [9, 10] и подтверждено машинным моделированием, проведенным автором. Результаты моделирования на ЭВМ динамики развития гаплоидных панмиктических популяций с неперекрывающимися поколениями приведены на рис.1.
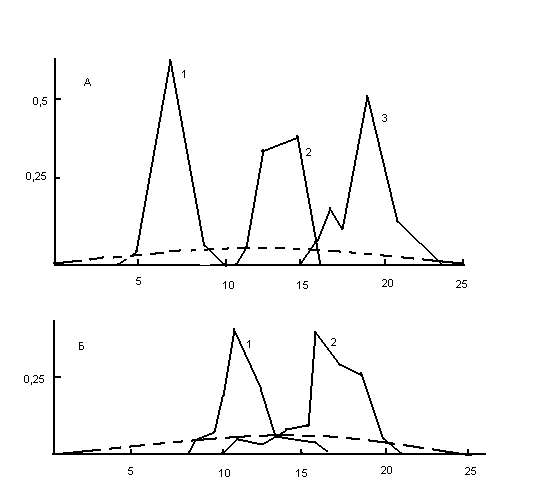
Рис.1.,
здесь, по оси X распределены численные значения блуждающего признака, а по оси Y доля этих значений в популяции.
Каждое новое поколение являлось результатом случайной выборки из совокупности потомков предыдущего.
Этот эффект приводит к тому, что в каждой дупликации, достижение значений, даже весьма отдаленных от начального, производится не единичной особью, но целой популяцией или, по крайней мере, ее значительной частью.
Как видно, в такой трактовке, вероятность выживания новых форм эквивалентна вероятности сохранения обычной точечной мутации типа замены основания в молекуле ДНК.
На основании дупликационной гипотезы и описанного эффекта группировки модификаций, можно построить достаточно полную модель эволюционного процесса. Ниже предлагается один из вариантов подобной модели.
Для более наглядного представления эволюционных изменений, связанных с преобразованием всего генома в целом, воспользуемся его преставлением в в многомерном пространстве Х возможных признаков. Будем считать, что каждый признак обладает некоторой дискретной мерой (шкалой значений), единой для всех признаков. Все особи одного вида обладают одним и тем же набором признаков, хотя их численные значения могут различаться. В этом случае, каждая особь, в её фенотипической форме, может быть представлена в пространстве признаков точкой х. Будем понимать расстояние между двумя точками как меру различия между двумя соответствующими этим точкам особями.
Каждой точке x(j) пространства Х может быть поставлена в соответствие некоторая функция R(j), численно выражающая приспособленность соответствующей этой точке «конструкции» организма к данным условиям среды. Далее мы будем использовать упрощенный вариант этой функции R(j) = V, если соответствующая «конструкция» жизнеспособна и R(j) = L в противном случае. Будем считать, что V-точки образуют в пространстве Х V-области, каждая из которых имеет более или менее четкую границу.
В свете приведенных определений, каждый вид занимает в Х обособленную область, являющуюся частью V-области или полностью совпадающую с ней. Области соответствующие разным видам не только не пересекаются, но и расположены достаточно далеко друг от друга. Это утверждение основано на определении расстояния между двумя точками как меры различия соответствующих им форм и постулировании того факта, что особи одного вида более схожи между собой, чем особи разных видов.
Можно предположить, что пространство между этими областями заполнено преимущественно L-точками. Действительно, трудно предположить, что большинство всевозможных сочетаний значений признаков соответствуют жизнеспособным признакам. Естественно считать жизнеспособные области островками в море нежизнеспособных комбинаций.
Дадим теперь интерпретацию эволюционного процесса в принятой нами системе дуплицированных признаков.
Пусть каждый признак имеет n-1 дублей (n-кратная дупликация).Вообще говоря, признаки могут иметь различное количество дублей, однако в целях упрощения ограничимся этим вариантом. Тогда в пространстве Х, каждой особи может соответство вать n^c (n в степени c) точек, где с – количество признаков данной особи. Одна из этих точек соответствует реальному фенотипу, в то время как остальные n^c-1 точек являются чисто информационными образованиями. Будем называть эти точки виртуальными. Одни из этих точек могут соответствовать реальным фенотипам с пониженной жизнеспособностью, другие «бессмысленным» сочетаниям признаков, т.е. находиться в L-области.
Иными словами, виртуальная точка, это часть генома, в которой некоторые локусы определяющие фенотипические признаки, заменены дублями.
Соответственно, реальной фенотипической популяции сопутствуют n^c-1 виртуальных популяций, каждая из который состоит из совокупности состоящих из одинаковых локусов виртуальных точек популяций. Отметим, что все эти популяции, фенотипическая и виртуальные могут, в разной степени, пересекаться друг с другом.
Точки, соответствующие фенотипической популяции, находятся под контролем естественного отбора и перемещаясь в Х за счет мутаций и рекомбинаций, группируются вокруг текущего оптимума соответствующей V-области. Поведение виртуальных точек будет иным.
Мы уже говорили о том, что значения нейтральных признаков блуждают по шкале их значений, в виде непрерывной компактной группы. Так как виртуальные популяции находятся вне контроля естественного отбора, все их признаки можно считать нейтральными. Поэтому они образуют в пространстве Х более или менее компактные множества точек, блуждающих в этом пространстве под действием мутаций и дрейфа.
В процессе блуждания виртуальные популяции могут проходить области соответствующие летальным L-точкам и точкам с пониженной приспособляемостью. Могут «наползать» на V-области причем, если эти V-области соответствуют «конструкциям» с большей приспособляемостью, чем фенотипические, может произойти замена фенотипов. Виртуальная популяция превратится в фенотипическую, а бывшая фенотипическая в виртуальную. Ввиду компактности виртуальных популяций, это явление будет носить массовый и быстрый, по эволюционным масштабам, характер. Внешний наблюдатель увидит, что в популяции начинают появляться особи, значительно отличающиеся от исходных. Здесь в физическом проявлении, эволюционный процесс носит скачкообразный характер, в то время как в информационном плане он непрерывен и достаточно длителен. Такая трактовка позволяет обойти многие затруднения, имеющиеся в классической эволюционной теории.
Так, традиционная интерпретация предполагает для каждого эволюционирующего признака наличие в пространстве признаков непрерывной траектории состоящей из жизнеспособных V-точек. Непрерывной, в том смысле, что V-точки разделяются расстояниями, соответствующими единичным мутациям. Причем, вдоль всей этой траектории должен существовать градиент, увеличивающий значение приспособленности. Как видим, здесь природе предъявлены значительно более жесткие требования чем в дупликационной модели, не требующей непрерывности эволюционной траектории.
Образование качественно новых признаков совершенно естественно для дупликационной модели. Собственно, дупликационная гипотеза и появилась, прежде всего, для объяснения подобного явления. [5, 6, 8].
Не вызывает затруднений, в данной модели, описание симпатрического дивергентного видообразования. Так, если какая-либо виртуальная популяция, в результате дрейфа, совместилась с V-областью, фенотипическое проявление которой не является конкурентным исходному виду, то возможно их параллельное развитие. Причем на первом этапе дивергирующие виды могут взаимно превращаться друг в друга. Это может происходить в том случае, когда вновь возникающие формы соответствуют крайним точкам V-области и могут быть выведены из нее обратными мутациями. В то же время, бывшая фенотипическая компонента еще не успела деградировать. Впоследствии виртуальная составляющая дивергировавших видов, не испытывая давления естественного отбора, будет искажаться мутациями, в результате чего произойдет необратимая генетическая изоляция этих форм. В дальнейшем они будут развиваться совершенно самостоятельно.
Рассмотрим теперь, как в рамках дупликационной модели объясняются описанные выше парадоксы скорости эволюции.
Так как при n-кратной дупликации одна мутация изменяет положение n^(c-1) виртуальных точек, то даже при не очень больших значениях n и c, будем иметь количество виртуальных форм, выражаемое поистине астрономическим числом. Естественно, что в этом случае основными факторами, влияющими на темп эволюции, будет именно это количество виртуальных форм. Влияние величины популяции и длительности репродуктивного цикла, по сравнению с ними пренебрежимо мало. Их единственная роль в эволюционном процессе – обеспечить воспроизведение популяции.
Поэтому, учитывая тот фактор, что с усложнением организмов растет число составляющих их признаков, темп эволюции будет в большей степени зависеть от сложности организмов, чем от их численности и длительности репродукционного цикла.
Неравномерность скорости эволюционного процесса, в данной модели, может быть объяснена следующим образом. Так как для каждой популяции достижение новой V-области явление достаточно редкое, то временные интервалы между двумя событиями такого рода будут значительными и соответственно разброс между ними может быть как угодно большим.
Перейдем теперь к рассмотрению одного важного свойства дупликационной модели. Оно связано с тем, что генетические процессы происходящие в виртуальной части генома, не проявляясь в фенотипе, недоступны прямому внешнему наблюдению. Можно предположить, что в случае какого-либо повреждения фенотипической составляющей генома, происходит переключение на оду из жизнеспособных виртуальных компонент. И если эта компонента состоит из не успевших измениться дублей, то изменения фенотипа не произойдет. Фактически сработает эффект резервирования. Это приводит, в свою очередь, к необходимости пересмотра таких понятий, как частота мутаций и плейотропия.
Действительно, для обнаружения мутаций обычно пользуются регистрацией внешних изменений или изменений поддающихся не очень сложным методам определения. В нашем случае внешние изменения будут сопутствовать далеко не каждой мутации. Поэтому истинная частота мутаций может быть значительно выше той, которая определяется описанными методами.
Эффект плейотропии также определяется по конечному результату, заключающемуся в наблюдении одновременного изменения группы признаков (в результате одной мутации). Однако тот же эффект будет наблюдаться и при фенотипическом проявлении виртуальной точки, если она разошлась с исходной фенотипической именно на эту комбинацию признаков.
Это же свойство позволяет дать новое толкование такому явлению как, получение новых форм воздействием мутагенных факторов. Пусть существует одна или несколько виртуальных популяций совмещенных с V-множествами отличными от фенотипического и соответствующих точкам с пониженной жизнеспособностью. При воздействии мутагена, у некоторых особей может быть повреждена фенотипическая часть генома, при этом остались не тронутыми какая-то часть описанных выше дупликаций. В результате, в популяции, появится группы одинаковых мутантов, каждая из которых, будет соответствовать одному из совмещенных с этими дупликациями V-множеств. Естественно, эти мутанты будут иметь пониженную жизнеспособность.
Важно отметить, что в каждой из этих групп повреждения генома могут быть в разных местах, главное чтобы осталась неповрежденной его дуплицированная часть. Полученные таким способом мутанты могут существенно отличаться от исходного типа, даже если сама мутация вызвала незначительные изменения генома.
Наличие потенциально жизнеспособных виртуальных точек может привести к их фенотипическому проявлению в результате изменений внешней среды, если какая-либо из них окажется более жизнеспособной в новых условиях. Здесь мы имеем своеобразный генетический вариант преадаптации. Заметим, что скорость реакции на изменение внешней среды, в этом случае будет зависеть не от частоты мутации, а от скорости срабатывания неизвестного нам механизма фенотипической части генома на виртуальную.
Подведем итоги и попытаемся определить место гипотезы дупликационной эволюции относительно классической эволюционной теории.
В классической теории принято считать, что видовые и надвидовые изменения обусловлены одними и теми же генетическими факторами и факторами отбора [2]. Разделение механизмов макро и микроэволюции отвергается большинством исследователей. В дупликационной модели такое разделение естественно. Здесь мы имеем два независимых процесса, один из которых фенотипический, проходит в соответствии с традиционным представлением об эволюции. Другой процесс развивается за счет мутаций и дрейфа дуплицированной части генома. Хотя по сути своей, этот процесс непрерывен, внешнему наблюдателю он представляется скачкообразными изменениями фенотипа. Причем, изменения эти могут быть довольно значительными.
Это дает нам основание считать, что первый из этих процессов является основой микроэволюции, в то время как второй, обеспечивая скачкообразные изменения фенотипа, соответствует понятию макроэволюции. Разница между этими двумя процессами именно в механизме протекания, а не в конечном результате. Так V-область может иметь размеры достаточные для весьма продолжительных и эффективных изменений. Примером может служить эволюция зубов и конечностей у лошади или хобота у слона. Подобная эволюция обычно называется направленной [11, 12]. В нашей классификации это соответствует микроэволюционному процессу, хотя и приводит к значительным изменениям.
Традиционная интерпретация большое место отводит эволюционным изменениям в ответ на изменения внешней среды [2, 11]. Пример – индустриальный меланизм березовой пяденицы. В дупликационной модели скачкообразные эволюционные изменения являются следствием достижения одной или несколькими виртуальными популяциями новой V-области. Такое достижение происходит случайно и независимо от внешней среды, которая только в этом случае производит выбор между старым и новым вариантами.
До сих пор мы акцентировали внимание на отличиях дупликационной модели эволюции от ее традиционного толкования. Теперь рассмотрим их общие моменты. Как известно, любая эволюционная гипотеза базируется на двух основных положениях – постулируемом механизме изменчивости и отношении к естественному отбору. В рассмотренной нами дупликационной модели первое положение полностью соответствует традиционным представлениям. Мелкие случайные отклонения в обоих случаях являются основным механизмом изменчивости. Более того, дупликационная модель даже меньше, чем традиционная гипотеза нуждается в каких-либо экзотических механизмах изменчивости для объяснения существующего многообразия жизни.
Что касается отношения к естественному отбору, то здесь дело обстоит сложнее. Без сомнения скрытая и, заметим, основная фаза эволюционного процесса – блуждание виртуальных популяций, происходит без участия естественного отбора, который однако вступает в действие при их фенотипическом проявлении. Выбор между новой фенотипической формой и ее старым вариантом принадлежит исключительно естественному отбору. Более того, имеются предположения, что сама дупликация связана с естественным отбором [5].
Скачкообразное появление новых форм сближает дупликационную модель с сальтационистскими представлениями. Однако предлагаемый генетический механизм их образования, сходный с традиционной концепцией, позволяет обойти наиболее уязвимое место сальтационизма – вероятность выживания этих новых форм.
Исходя из сказанного, дупликационную модель, в том виде, как она здесь представлена, нужно понимать как объединение традиционной эволюционной теории и сальтационистских концепций.
Автор выражает благодарность канд. биол. наук Б.А. Калабушкину за обсуждение и редакцию рукописи.
Литература:
1. Левонтин Р. Генетические основы эволюции. М.: Мир, 1978, 349 с.
2. Майр Э. Популяции, виды, эволюция. М.: Мир, 1974, 460 с.
3. Шварц С.С. Экологические закономерности эволюции. М.: Наука 1983, 276 с.
4. Галл Я.М. Истоки эволюционной экологии: конкуренция, естественный отбор, видообразование. // Природа 1985, № 11, с. 67
5. Оно С. Генетические основы прогрессивной эволюции. М.: Мир, 1973, 227 с.
6. Алтухов Ю.П. Генетические процессы в популяциях. М.: Наука, 1983, 276 с.
7. Кимура М. Молекулярная эволюция: теория нейтральности. М.: Мир, 1986, 398 с.
8. Бейссон Ж. Генетика. М.: Атомиздат, 1976, 126 с.
9. Ohta T. Kimura M. A model of mutation appropriate to estimate the number of electrophoretically detectable alleles in a finite populations // Genet. Res. 1973 Vol. 22. P. 201-204
10. Ohta T. Kimura M. Simulation studies on electrophoretically detectable genetic variability in a finite populations // Genet. 1974, Vol. 76. P. 615-824
11. Грант В. Эволюция организмов. М.: Мир, 1980, 407 с.
12. Дубинин Н.П. Новое в современной генетике. М.: Наука, 1986, 220 с.
Опубликовано в сборнике:
Информационные проблемы современной биологии. Математическое моделирование природных систем. – М. Наука, 1992 с. 170.
Работы на эту тему:
Компьютерное моделирование дивергентной эволюции в однородной среде





